Four researchers– Anirudh Subramanyam, Jacob Roth, Albert Lam and Mihai Anitescu – have won the Best Publication Award in Energy for 2023 from the Energy, Natural Resources, and the Environment Section of INFORMS for their paper “Failure probability constrained AC optimal power flow.”
The ENRE Best Publication Awards are given annually to the best refereed journal articles in the areas of interest to ENRE, published two calendar years prior to the year in which the award is given.
The paper by the Argonne team was published in IEEE Transactions on Power Systems in November 2022. The four authors all were members of Argonne’s Mathematics and Computer Science (MCS) division at the time the paper was submitted. Anitescu is a senior computational mathematician in the MCS division; Subramanyam is now on the faculty at Penn State, Roth is a graduate student at the University of Minnesota, and Lam is a data scientist at Moderna.
The award-winning paper addresses a key problem facing the power grid: blackouts due to cascading failures in power transmission systems.
Numerous tools have been developed to restrict the propagation of a cascading failure, but these generally apply after severe contingencies have occurred. Simulation-based tools also have been used to devise long-term cascade mitigation solutions, but these tend to be limited in preventing cascade in short-term operations.
The standard technique used to address the cascading risk problem is called ACOPF – alternating current optimal power flow formulation. While myriad enhancements have been added to ACOPF since its introduction in the early 1960s, the problem remains extremely time consuming.
To address this situation, the Argonne team developed an analytical approach that models the cascade severity as an explicit function of the network properties and dispatch point.
“Our aim is to design a dispatch point that has a low operator-specified likelihood of triggering a cascade starting from any single component outage,” said Anitescu. “By delaying the system’s first failure time, FP-ACOPF is able to delay – and hence prevent – subsequent line failures that could lead to system collapse.”
The approach, which the researchers call failure probability-constrained ACOPF, or FP-ACOPF, generalizes the standard ACOPF method by using techniques from bilevel optimization and numerical linear algebra to reformulate the probability constraints algebraically.
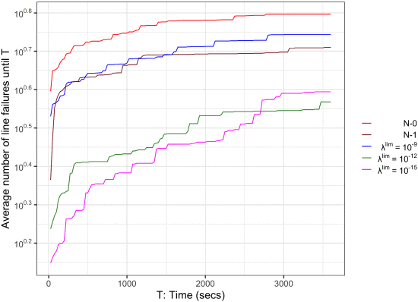
Simulation results show that FP-ACOPF can significantly outperform both unconstrained and security-constrained ACOPF models, reducing the probability of long severe cascades and large demand losses, without incurring significantly larger computational or economic costs. Figure 1, for example, shows that in the first 15 minutes after the first failure, FP-ACOPF with a failure rate limit λlim = 10−15 has about two times fewer line failures than does the security-constrained (N-1) ACOPF.
“Our approach allows us to explore the trade-offs between cascade potential, dispatch costs and operator conservatism without significant increase in computational complexity,” Anitescu said.
He and his colleagues see the work as a first step toward quantifying and proactively reducing failure risk – and implicitly, cascading risk – in operational dispatch.
For the full paper, see Anirudh Subramanyam, Jacob Roth, Albert Lam and Mihai Anitescu, “Failure probability constrained AC optimal power flow,” IEEE Transactions on Power Systems 37(6) 4683-4695, Nov. 2022, at the website https://ieeexplore.ieee.org/abstract/document/9695256.
