Researchers from Argonne National Laboratory and the University of Wisconsin-Madison have received the Mathematical Programming Computation “Outstanding Paper of the Year” award for 2022. This was the second year in a row that Argonne researchers have won the award.
This year’s award-winning paper presents a graph-based modeling abstraction for optimization that exploits the problem structure to solve complex problems. A key novelty of this abstraction (known as an “OptiGraph”) is that any optimization problem is treated as a hierarchical hypergraph of nodes and edges. Each node contains an optimization model with its own variables, constraints, objectives and data; and edges capture connectivity between the node models.
“The beauty of our abstraction is its flexibility,” said Victor Zavala, a senior computational mathematician in Argonne’s Mathematica and Computer Science (MCS) Division and Baldovin-DaPra Professor in the College of Engineering at the University of Wisconsin-Madison. “The OptiGraph captures both algebraic and object-oriented modeling paradigms in the same framework; it enables modular construction; and it facilitates the use of powerful graph analysis tools for visualizing, analyzing and manipulating the model structure.”
The researchers demonstrate the modularity of their abstraction using a large, dynamic optimization problem for a natural gas network involving multiple gas supplies, pipelines, and compressor stations. The network is modeled as a stand-alone OptiGraph with nodes distributed over time and then connected as a high-level graph to form the complete problem.
“The modular construction is one of the benefits of the graph abstraction,” said Jordan Jalving, a senior engineer at Pasteur Labs, a former Ph.D. student of Zavala at the University of Wisconsin–Madison, and a former research intern at Argonne. “Specific component models can be developed separately, and the syntax of the components can be different because each OptiGraph is a self-contained object. This greatly facilitates model construction and debugging.”
One approach to using an OptiGraph is to divide it into partitions, construct new subgraphs from the partitions, and derive a new representation of the OptiGraph. Determining effective partitions is not a trivial task, however. The researchers implemented the OptiGraph abstraction in Plasmo.jl, a Julia language package that provides interfaces with standard graph partitioning tools. They then used the capabilities of Plasmo.jl to experiment with different partitioning strategies and to analyze trade-offs between coupling, imbalance, and memory use.
A central problem is computational load balancing. To demonstrate the criticality of the partitions, the research team explored different partition strategies with different imbalances. For example, with 24 partitions, increasing the imbalance can result in ill-conditioned problems with diminished performance, whereas with 48 partitions, increasing the imbalance results in computational improvement (see Fig. 1).
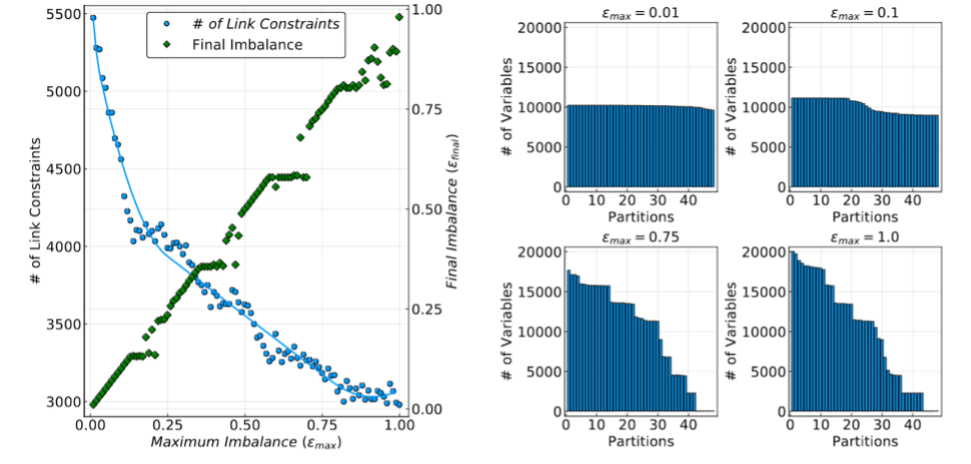
Fig. 1: Left: Effect of increasing the imbalance for the 48-partition case on the true final imbalance the partitioner produced and the total number of linking constraints. Nominal values of maximum imbalance (less than 25%) reduce the number of linking constraints considerably, but greater values produce diminishing returns. Right: Distribution of subproblem sizes for a few maximum imbalance values. Under naive partitioning, the size of the partitions can vary by an order of magnitude. (Source: J. Jalving)
“Here, again, flexibility is important,” said Sungho Shin, a postdoctoral appointee in Argonne’s MCS Division and a former Ph.D. student of Zavala. “Flexible partitions can help fit the solver to the computing architecture of interest.”
Zavala noted that “the research has made us realize the many ways in which graph theory can be used to model, analyze, and solve large optimization problems.” Future efforts will focus on more customized graph partitioning tools and parallel modeling solvers that open promising directions for future research and problem-solving.
Work for the award-winning paper was carried out in part through the Argonne-led MACSER (Mathematics for Rare, High Impact Events in Complex Energy and Environment Systems) project. For the full paper, see Jalving, J., Shin, S. & Zavala, V.M. A graph-based modeling abstraction for optimization: concepts and implementation in Plasmo.jl. Math. Prog. Comp. 14, 699–747 (2022). https://doi.org/10.1007/s12532-022-00223-3
